Dataset

Creating a Custom Dataset

A custom Dataset class must implement 3 functions: _init_, _len_, and _getitem_.

The implementation below:

the FashionMNIST images ar stored in a directory img_dir
the labels are stored separatedly in a CSV file

import os
import pandas as pd
from torchvision.io import read_image

class CustomImageDataset(Dataset):
    def __init__(self, annotations_file, img_dir, transform=None, target_transform=None):
        self.img_labels = pd.read_csv(annotations_file)
        self.img_dir = img_dir
        self.transform = transform
        self.target_transform = target_transform

    def __len__(self):
        return len(self.img_labels)

    def __getitem__(self, idx):
        img_path = os.path.join(self.img_dir, self.img_labels.iloc[idx, 0])
        image = read_image(img_path)
        label = self.img_labels.iloc[idx, 1]
        if self.transform:
            image = self.transform(image)
        if self.target_transform:
            label = self.target_transform(label)
        return image, label

_init_

函数__init__ 只在创建数据集实例的时候被调用。

初始化列表包括：

图像
标签连标文件
两者的转换器（transforms）

import os
import pandas as pd
from torchvision.io import read_image

class CustomImageDataset(Dataset):
    def __init__(self, annotations_file, img_dir, transform=None, target_transform=None):
        self.img_labels = pd.read_csv(annotations_file)
        self.img_dir = img_dir
        self.transform = transform
        self.target_transform = target_transform

    def __len__(self):
        return len(self.img_labels)

    def __getitem__(self, idx):
        img_path = os.path.join(self.img_dir, self.img_labels.iloc[idx, 0])
        image = read_image(img_path)
        label = self.img_labels.iloc[idx, 1]
        if self.transform:
            image = self.transform(image)
        if self.target_transform:
            label = self.target_transform(label)
        return image, label

_len_

_len_函数返回数据集中的数目
Ex：

1 2	def __len__(self): return len(self.img_labels)

_getitem_

_getitem_函数根据 索引idx 加载和返回对应样本。

Based on the index, it identifies the image’s location on disk, converts that to a tensor using read_image, retrieves the corresponding label from the csv data in self.img_labels, calls the transform functions on them(if applicable), and returns the tensor image and corresponding label in a tuple.

def __getitem__(self, idx):
    img_path = os.path.join(self.img_dir, self.img_labels.iloc[idx, 0])
    image = read_image(img_path)
    label = self.img_labels.iloc[idx, 1]
    if self.transform:
        image = self.transform(image)
    if self.target_transform:
        label = self.target_transform(label)
    return image, label

Preparing data for training with DataLoaders

Dataset返回数据集的特征与标签，但是在训练模型的时候，我们经常需要传递一个“minibatches”规模的样本，并且在每个epoch的时候 shuffle，减少模型的过拟合，以及利用 Python 的 multiprocessing来加速检索

DataLoader is an iterable that abstracts this complexity for us in an easy API.

from torch.utils.data import DataLoader

train_dataloader = DataLoader(training_data, batch_size=64, shuffle=True)
test_dataloader = DataLoader(test_data, batch_size=64, shuffle=True)

Iterate through the DataLoader

We have loaded that dataset into the DataLoader and can iterate through the dataset as needed. Each iteration below returns a batch of train_features and train_labels (containing batch_size=64 features and labels respectively). Because we specified shuffle=True, after we iterate over all batches the data is shuffled (for finer-grained control over the data loading order, take a look at Samplers).

# Display image and label.
train_features, train_labels = next(iter(train_dataloader))
print(f"Feature batch shape: {train_features.size()}")
print(f"Labels batch shape: {train_labels.size()}")
img = train_features[0].squeeze()
label = train_labels[0]
plt.imshow(img, cmap="gray")
plt.show()
print(f"Label: {label}")

Transforms

transforms 用来对数据集进行预处理，以使其适合训练或者进行一些图形处理。

transform: to modify the features
traget_transform: to modify the labels

The torchvision.transforms module offers several commonly-used transforms out of the box.

The FashionMNIST features are in PIL Image format, and the labels are integers.

To make these transformations, we use ToTensor and Lambda.

import torch
from torchvision import datasets
from torchvision.transforms import ToTensor, Lambda

ds = datasets.FashionMNIST(
    root="data",
    train=True,
    download=True,
    transform=ToTensor(),
    target_transform=Lambda(lambda y: torch.zeros(10, dtype=torch.float).scatter_(0, torch.tensor(y), value=1))
)

ToTensor()

ToTensor converts a PIL image or NumPy ndarray into a FloatTensor. and scales the images’s pixel intensity values in the range

Lambda Transforms

Lambda transforms apply any user-defined lambda function.

1
2
3

# we define a function to turn the integer into a one-hot encoded tensor. It first creates a zero tensor of size 10 (the number of labels in our dataset) and calls scatter_ which assigns a value=1 on the index as given by the label y.
target_transform = Lambda(lambda y: torch.zeros(
    10, dtype=torch.float).scatter_(dim=0, index=torch.tensor(y), value=1))

Automatic Diff with TORCH.AUTOGRAD

To compute those gradients, PyTorch has a built-in differentiation engine called torch.autograd.
It supports automatic computation of gradient for any computational graph.
Consider the simplest one-layer neural network, with input x, parameters w and b, and some loss func. It can be defined in PyTorch in the following manner:

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

Tensors, Functions and Computational graph

This code defines the following computational graph:

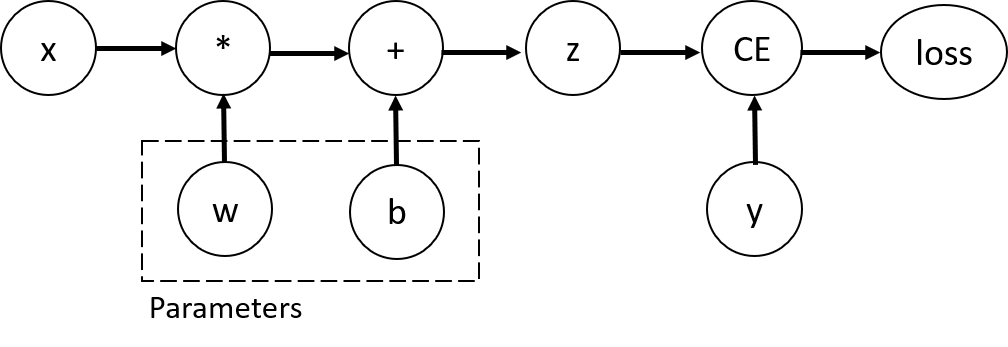
In this network,andare parameters, which we need to optimize.
we need to compute the gradients of loss func with respect to those variables.(set the requires_grad property of those tensors)

You can set the value of requires_grad when creating a tensor, or later by using x.requires_grad_(True) method.

A func that we apply to tensors to construct computational graph is in fact an object of class Func. This object knows how to compute the func in the forward direction, and also how to compute its derivative during the backward propagation step. A reference to the backward propagation func is stored in grad_fn property of a tensor.

我们用来构造计算图（pipeline）的函数，实际上就是一个 函数类 的对象。
该对象知道如何 正向计算 函数，也知道如何计算其微分通过 反向传播 的步骤
关于 反向传播 函数被存储在了一个张量的 grad_fn 属性中。

1 2	print(f"Gradient function for z = {z.grad_fn}") print(f"Gradient function for loss = {loss.grad_fn}")

Computing Gradients

To optimize weights of parameters in the neural network, we need to compute the derivatives of our loss function with respect to parameters, namely, we needandunder some fixed values ofand. To compute those derivatives, we call loss.backward(), and then retrieve the values from w.grad and b.grad:

1
2
3

loss.backward()
print(w.grad)
print(b.grad)

We can only obtain the grad properties for the leaf nodes of the computational graph, which have requires_grad property set to True. For all other nodes in our graph, gradients will not be available.
We can only perform gradient calculations using backward once on a given graph, for performance reasons. If we need to do several backward calls on the same graph, we need to pass retain_graph=True to the backward call.

Disablling Gradient Tracking

By default, all tensors with requires_grad=True are tracking their computational history and support gradient computation.
However, there are some cases when we do not need to do that, for example, when we have trained the model and just want to apply it to some input data, i.e. we only wanna do forward computations through the network.

torch.no_grad() block

stop tracking computations by surrounding our computation code with torch.no_grad() block:

z = torch.matmul(x, w) + b
print(z.requires_grad)

with torch.no_grad():
    z = torch.matmul(x, w) + b
print(z.requires_grad)

detach()

1
2
3

z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)

There are reasons you might want to disable gradient tracking:

To mark some parameters in your neural network as frozen parameters. This is a very common scenario for finetuning a pretrained network
To speed up computations when you are only doing forward pass, because computations on tensors that do not track gradients would be more efficient.

More on Computational Graphs

Conceptually, autograd keeps a record of data (tensors) and all executed operations (along with the resulting new tensors) in a directed acyclic graph (DAG) consisting of Function objects.
In this DAG, leaves are the input tensors, roots are the output tensors. By tracing this graph from roots to leaves, you can automatically compute the gradients using the chain rule.

In a forward pass, autograd does two things simultaneously:

run the requested operation to compute a resulting tensor
maintain the operation’s gradient function in the DAG.

The backward pass kicks off when .backward() is called on the DAG root(最后的结点). autograd then:

computes the gradients from each .grad_fn
accumulates them in the respective tensor’s .grad attribute
using the chain rule, propagates all the way to the leaf tensors.

DAGs are dynamic in PyTorch An important thing to note is that the graph is recreated from scratch; after each .backward() call, autograd starts populating a new graph. This is exactly what allows you to use control flow statements in your model; you can change the shape, size and operations at every iteration if needed.

Tensor Gradients and Jacobian Products

In many cases, we have a scalar loss function, and we need to compute the gradient with respect to some parameters.
However, there are cases when the output function is an arbitrary tensor.
In this case, PyTorch allows you to compute so-called Jacobian product, and not the actual gradient.

For a vector function, whereand, a gradient ofwith respect tois given by Jacobian matrix:

Instead of computing the Jacobian matrix itself, PyTorch allows you to compute Jacobian Product $𝕧$ for a given input vector. This is achieved by calling backward withas an argument. The size ofshould be the same as the size of the original tensor, with respect to which we want to compute the product:

inp = torch.eye(5, requires_grad=True)
out = (inp+1).pow(2)
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"First call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")

Notice

when we call backward for the second time with the same argument, the value of the gradient is different.
This happens because when doing backward propagation, PyTorch accumulates the gradients, i.e. the value of computed gradients is added to the grad property of all leaf nodes of computational graph. If you want to compute the proper gradients, you need to zero out the grad property before. In real-life training an optimizer helps us to do this.

Previously we were calling backward() function without parameters. This is essentially equivalent to calling backward(torch.tensor(1.0)), which is a useful way to compute the gradients in case of a scalar-valued function, such as loss during neural network training.